Question

Q13. A stone is dropped from a height of 5 km. The distance it falls through varies directly with the

square of the time taken to fall through that distance. If it falls 64 min 4 seconds. find the distance the
stone covers in the 5th second?
A. 36 m
B. 58 m
C. 72 m
D. 100 m

Answer 1

I’m not sure but I think it might be C so sorry if it’s wrong

Answer 2

The stone covers 36 m in the 5th second. Correct choice: A.

Explanation:

Proportions

Two variables are said to be proportional if one of them can be calculated by multiplying the other by a constant of proportionality. If y and x are those variables, then:

y=k.x

There are other similar proportions where the relation is not linear. For example, if y is proportional to the square of x, then:

`y=k.x^2`

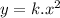
According to the conditions of the question, the distance traveled by a stone dropped from a height of 5 Km varies directly with the square of the time taken to fall through that distance. If d is the distance and t is the time, then;

`d=k.t^2`

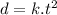
To find the value of k, we use the given condition: The stone falls d=66 meters in t=4 seconds. Substituting:

`64=k.4^2=16k`

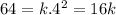
Solving:

`k=64/16=4`

Substitute the value of k into the equation to get the complete model.

`d=4.t^2`

Now we calculate the distance when t=5 seconds:

`d=4\cdot 5^2=4\cdot 25=100`

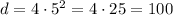
The stone has covered 100 m in 5 seconds. But we need to find the distance covered in the 5th second, that specific interval between 4 sec and 5 sec.

Since we already know the distance for t=4 sec (64 m), and the distance for t=5 sec (100 m), then:

distance in the 5th second = 100 m - 64 m = 36 m

The stone covers 36 m in the 5th second. Option A.