Question

A bowl of fruit contains seven pieces of fruit, including two bananas and five apples. Three pieces of fruit are chosen. What is the probability that one banana and two apples are chosen?

Answer 1

Or 57.14%

Explanation:

Answer 2

`(4)/(7)`

Explanation:

A combination refers to the selection of objects such that order does not matter. A permutation refers to the arrangement of objects such that order do matter.

Number of bananas = 2

Number of apples = 5

One banana and two apples are chosen.

So,

probability that one banana and two apples are chosen =
`(C(2,1)\,C(5,2))/(C(7,3))`

`C(2,1)=(2!)/(1!(2-1)!)=2`

`C(5,2)=(5!)/(2!(5-2)!)=(5!)/(2!31) =10`

`C(7,3)=(7!)/(3!(7-3)!) =(7!)/(3!4!)=35`

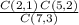
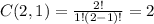
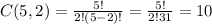
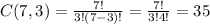
So,

Probability that one banana and two apples are chosen =
`(2(10))/(35)=(4)/(7)`