Answer: $98,835.
Explanation:
Given: Annual profit at a chain of stores is normally distributed with a mean (
 ) of $61,000 and a standard deviation(
) of $61,000 and a standard deviation(
 ) of $23,000.
) of $23,000.
Let
 denoted the profit.
denoted the profit.
Let
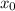 be the minimum profit required to have a party.
be the minimum profit required to have a party.
The stores in the top 5% (i.e. 0.05) of annual profit were rewarded with a celebration.
i.e.
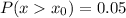
![\Rightarrow\ P((x-\mu)/(\sigma)>(x_0-61000)/(23000))=0.05\\\\\Rightarrow\ P(z>(x_0-61000)/(23000))=0.05\ \ \ [z=(x-\mu)/(\sigma)]\\\\\Rightarrow\ (x_0-61000)/(23000)=1.645\ \ [\text{critical z-value for p-value 0.05=1.645}]\\\\\Rightarrow\ x_0-61000 =1.645* 23000\\\\\Rightarrow\ x_0-61000 =37835\\\\\Rightarrow\ x_0=37835+61000\\\\\Rightarrow\ x_0=98835](https://img.qammunity.org/2021/formulas/mathematics/high-school/khgzqwy16a5u0o0ojdexl5pduvngug3aut.png)
Hence, the annual profit required to have a party was $98,835.