Answer:

Explanation:
The other user posted a great answer, but I would like to show you a more mathematical way!
We have
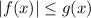 .
.
By the definition of absolute value, this is the same as saying:
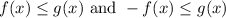
For the right, we can divide both sides by -1 to acquire:
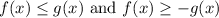
We can now combine them. This yields:
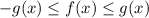
Now, we can use the Squeeze Theorem (a.k.a. Pinch or Sandwich Theorem). The Squeeze Theorem posits that if we have:
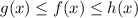
And:
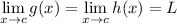
Then the following must be true:
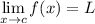
We have:
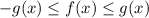
And we know that:

Then it follows that:
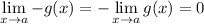
Therefore, by using the Squeeze Theorem, we can conclude that:

And we're done!