Question

Which expression is a prime polynomial, x^3-1, x^2+1, x^3+1, x^2-1

Answer 1

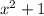`x^2+1` cannot be factored, thus it's a prime polynomial

Explanation:

A prime number or expression cannot be factored in any factor different from 1 and the number or expression itself.

One of the following expressions is prime. The rest of them can be factored.

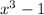`x^3-1` is the difference of two cubes. It can be factored as:

`x^3-1=(x-1)(x^2+x+1)`

`x^3+1` is the sum of two cubes. It can be factored as:

`x^3+1=(x+1)(x^2-x+1)`

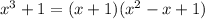
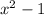`x^2-1` is the difference of two squares. It can be factored as:

`x^2-1=(x-1)(x+1)`

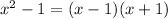
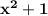`\mathbf{x^2+1}` cannot be factored, thus it's a prime polynomial