Answer:
-2/3
Step-by-step explanation:
Here, we need to rearrange the equation into slope intercept form:
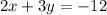
subtract 2x on both sides:
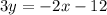
divide 3 on both sides:
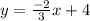
Finally, we get it in the form y = mx + b. We know that in that form, m is the slope so that means, the slope is -2/3