Question

Given the domain {-4, 0, 5}, what is the range for the relation 12x + 6y = 24?

A.
{-4, 4, 14}
B.
{2, 4, 9}
C.
{-12, -4, 6}
D.
{12, 4, -6}

Answer 1

The answer is down below have a good day!!!

Answer 2

The range is {12, 4, -6} ⇒ D

Explanation:

The range of the relation is the values of y corresponding to the values given for x which is the domain of the relation

∵ The relation is 12x + 6y = 24

∵ The domain of the function is {-4, 0, 5}

→ That means x = -4, 0, 5, we need to find their corresponding values of y

∴ Substitute the values of x in the relation

∵ x = -4

∴ 12(-4) + 6y = 24

∴ -48 + 6y = 24

→ Add 48 to both sides

∴ -48 + 48 + 6y = 24 + 48

∴ 6y = 72

→ Divide both sides by 6 to find y

∴
`(6y)/(6)=(72)/(6)`

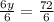
∴ y = 12

∵ x = 0

∴ 12(0) + 6y = 24

∴ 0 + 6y = 24

∴ 6y = 24

→ Divide both sides by 6 to find y

∴
`(6y)/(6)=(24)/(6)`

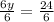
∴ y = 4

∵ x = 5

∴ 12(5) + 6y = 24

∴ 60 + 6y = 24

→ Subtract 60 from both sides

∴ 60 - 60 + 6y = 24 - 60

∴ 6y = -36

→ Divide both sides by 6 to find y

∴
`(6y)/(6)=(-36)/(6)`

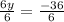
∴ y = -6

∵ The range is the values of y which corresponding to the domain

∴ The range is {12, 4, -6}