Question

How do you do this question?

Answer 1

Answers:

`\displaystyle \lim_(n \to \infty) (a_n)/(b_n) = 6`

Based on the limit comparison test, the series is convergent

========================================================

Step-by-step explanation:

As n gets really large, the terms
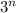`3^n` and
`3^n-2` are effectively the same. Taking the limit to infinity of the ratio leads to 1.

In other words,

`\displaystyle \lim_(n \to \infty) (3^n)/(3^n-2) = \lim_(n \to \infty) (3^n)/(3^n) = 1`

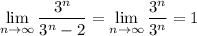
That -2 doesn't really play a role when n gets very large.

This result is then multiplied by the 6 in the
`a_n` sequence, getting 6 as the final limit we want.

So,

`L = \displaystyle \lim_(n \to \infty) \left(a_n / b_n\right)\\\\\\L = \displaystyle \lim_(n \to \infty) \left((6)/(3^n-2) / (1)/(3^n)\right)\\\\\\L = \displaystyle \lim_(n \to \infty) \left((6)/(3^n-2) * (3^n)/(1)\right)\\\\\\L = \displaystyle \lim_(n \to \infty) \left((6*3^n)/(3^n-2)\right)\\\\\\`

`L = \displaystyle 6*\lim_(n \to \infty) \left((3^n)/(3^n-2)\right)\\\\\\L = \displaystyle 6*\lim_(n \to \infty) \left((3^n)/(3^n)\right)\\\\\\L = \displaystyle 6*\lim_(n \to \infty) (1)\\\\\\L = \displaystyle 6*1\\\\\\L = \displaystyle 6\\\\\\`

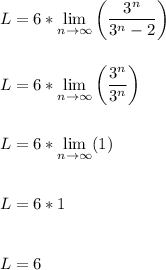
Since the limiting value is positive and not infinity, this means that both series
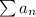`\sum a_n` and
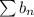`\sum b_n` converge or they both diverge.

----------------------------

If we plug n = 2 into the
`b_n` sequence, we get

`b_n = (1)/(3^n)\\\\b_2 = (1)/(3^2)\\\\b_2 = (1)/(9)`

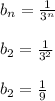
The first term is a = 1/9

If we plugged n = 3, we would get
`b_3 = (1)/(27)`

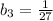
This shows that the common ratio is r = 1/3

Because -1 < r < 1 is true, we know that the infinite geometric series converges. Therefore,
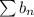`\sum b_n` converges. We don't need to find the converging value.

Going back to the limit comparison test, we stated that both
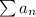`\sum a_n` and
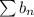`\sum b_n` either diverge together or converge together.

We've shown that the b series converges, so the 'a' series must converge as well.