Answer:
Options (A) and (C)
Explanation:
From table attached,
Let the equation of a linear equation that represents the input-output values in the table is,
y - y' = m(x - x')
Where (x', y') is a point lying on the graph.
And m = slope of the line passing through two points
 and
and

m =
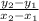
Slope of the line passing through (0, 11) and (1, 5) will be,
m =
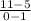
m = -6
Therefore, equation of the line passing through (0, 11) and slope = -6 will be,
y - 11 = -6(x - 0)
Equation of a line passing through (1, 5) and slope = -6 will be,
y - 5 = -6(x - 1)
Equation of a line passing through (2, -1) and slope = -6 will be,
y + 1 = -6(x - 2)
Equation of a line passing through (3, -7) and slope = -6 will be,
y + 7 = -6(x - 3)
Therefore, Options (A) and (C) are the correct options.