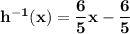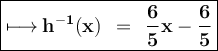Question

Pls help me ASAP PLS PLS PLS

Answer 1

Given :

• A linear function is given to us .
• The function is h(x) = ⅚x + 1 .

To Find :

• The inverse of the linear function that is h -¹ (x) .

Solution :

Given function to us is : ⅚ x + 1 .

Here is step by step explanation :

Step 1 : Replace h(x) with y .

The equation becomes ,

⇒ y = ⅚x + 1 .

Step 2 : Interchange the variables .

⇒ x = ⅚y + 1.

Step 3 : Solve for y .

⇒x = ⅚ y + 1.

⇒ x - 1 = ⅚y .

⇒ y = 6/5 ( x - 1 )

⇒ y = 6/5x - 6/5 .

Step 4 : Replace y again with
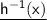
`\underline{\sf h^(-1)(x)}`

⇒
`\bf h^(-1)(x)=(6)/(5)x-(6)/(5)`

`\large\boxed{\red{\bf \purple{\longmapsto}\:h^(-1)(x)\:\:=\:\:(6)/(5)x-(6)/(5)}}`