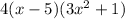Answer:
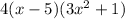
Explanation:
1) Find the Greatest Common Factor (GCF).
1 - What is the largest number that divides evenly into
 and
and
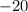 ?
?
It is
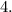
2 - What is the highest degree of
 that divides evenly into
that divides evenly into
 and
and
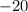 ?
?
It is 1, since
 is not in every term.
is not in every term.
3 - Multiplying the results above,
The GCF is 4.
2) Factor out the GCF. (Write the GCF first. Then, in parentheses, divide each term by the GCF.)
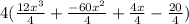
3) Simplify each term in parentheses.

4) Factor out common terms in the first two terms, then in the last two terms.

5) Factor out the common term
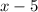 .
.