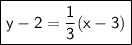Given : A line passes through a point ( 3 , -2 ) and the slope of the line is ⅓ .
To Find : The equation of that line .
Solution : Here we are provided with a point ( 3 , -2 ) and slope of the line which is ⅓ . So clearly here to represent the line we will use point - slope form , which is ;
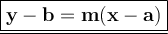
Where ,
- a is x - coordinate.
- b is y - coordinate .
- m is the slope of the line .
Here ,
Now , put the respective values ;