Question

1. The total monthly cost, y, for smartphone service depends

on the number of text messages,
Text Messages, X:
0
10
20
30
Cost ($), y
40.00
42.00
44.00 46.00
slope:
y-intercept:
equation:

Answer 1

• (0,40)
• (10,42)
• (20,44)
• (30,46)

Slope

• m=42-40/10
• m=2)10
• m=1/5

Equation in point slope form

• y-40=1/5x
• y=1/5x+40

slope=1/5

y intercept=40

Answer 2

`\textsf{slope}=(1)/(5)`

`\textsf{Equation}: \quad y=(1)/(5)x+40`

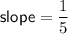
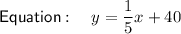
y-intercept = 40

Explanation:

`\large \begin{array}\cline{1-2} \sf Text\:Messages\: & \sf Cost (\$) \\x& y \\\cline{1-2} 0 & 40.00\\\cline{1-2} 10 & 42.00\\\cline{1-2} 20 & 44.00\\\cline{1-2} 30 & 46.00\\\cline{1-2}\end{array}`

Take two ordered pairs from the table:

`\textsf{let}\:(x_1,y_1)=(0, 40)`

`\textsf{let}\:(x_2,y_2)=(10, 42)`

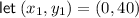
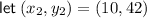
Substitute them into the slope formula and solve for m:

`\textsf{slope}\:(m)=(y_2-y_1)/(x_2-x_1)=(42-40)/(10-0)=(1)/(5)`

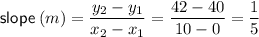
Use the point-slope form of a linear equation with the found value of m and the point (0, 40):

`\implies y-y_1=m(x-x_1)`

`\implies y-40=(1)/(5)(x-0)`

`\implies y=(1)/(5)x+40`

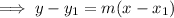
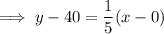
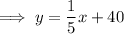
Slope-intercept form of a linear equation:
`y=mx+b`

(where m is the slope and b is the y-intercept).

Comparing with the calculated equation:

y-intercept = 40