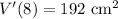Question

The volume of a cube with sides of length s is given by V = s^3. Find the rate of change of the volume with respect to s when s = 8 centimeters.​

Answer 1

`V'(8)=192\text{ cm}^2`

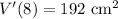
Explanation:

We have the volume of a cylinder:

`V=s^3`

To find the rate of change of the volume with respect to s, we will take the derivative of both sides with respect to s. So:

`(d)/(ds)[V]=(d)/(ds)[s^3]`

Differentiate. Use the power rule:

`V'(s)=3s^2`

So, to find the rate of change of the volume when s is 8 centimeters, substitute 8 for s:

`V'(8)=3(8)^2`

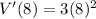
Evaluate:

`V'(8)=192\text{ cm}^2`