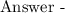
- Given - two points , say A with coordinates ( -10 , -8 ) and B with coordinates ( -5 , 4 )
- To calculate - distance between the two points
The distance formula states that
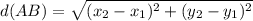
from the question , we can make out that
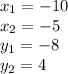
substituting the values in the formula , we get
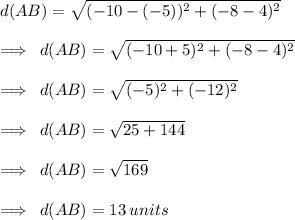
therefore , option 3) 13 is correct !
hope helpful ~