Question

Whatis the tigonemtric form of -3+4i

Answer 1

`z=5(\cos(2.214) + i\sin(2.214))`

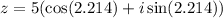
Explanation:

The trigonometric form (polar form) of a complex number x + yi is given by:

`z=r(\cos(\theta) + i\sin(\theta))`

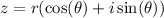
where:

• r is the magnitude (modulus) of the complex number.
• θ is the argument of the complex number.

The magnitude (r) can be calculated using the formula:

`r= |z|=√(x^2 + y^2)`

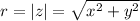
In this case, x = -3 and y = 4, so:

`\begin{aligned}r &=|-3+4i|\\&= √((-3)^2 + (4)^2) \\&= √(9 + 16) \\&= √(25) \\&= 5\end{aligned}`

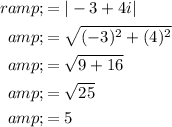
Now, find the argument (θ) by using the arctangent function:

`\theta = \arctan\left((y)/(x)\right)`

`\theta = \arctan\left((4)/(-3)\right)`

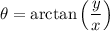
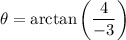
As θ is in quadrant II, we need to add π:

`\theta =\arctan\left((4)/(-3)\right)+\pi`

`\theta = 2.21429743...\; \rm rad`

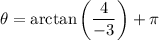
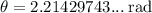
So, the trigonometric form of -3 + 4i where θ is measured in radians is:

`z=5(\cos(2.214) + i\sin(2.214))`

`\hrulefill`

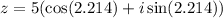
Additional notes

If you want θ measured in degrees, the trigonometric form is:

`z=5(\cos(126.87^(\circ)) + i\sin(126.87^(\circ)))`

Answer 2

We calculate the module:

`|z|\: = \: \sqrt{( - 3) ^(2) \: + \: {4}^(2) }`

`|z| \: = \: √(9 \: + \: 16)`

`|z| \: = \: √(25)`

`\boxedz`

We calculate the angle formed by "z":

`\arctan( (4)/( - 3) ) \: = \: \underline{0.92729521 \: \text{rad}}`

We pass it to degrees:

`0.92729521 \: * \: (180)/(\pi)`

`(166.91313924)/(\pi)`

`(166.91313924)/(3.14159265)`

`\boxed{ 53.13°}`

Now we use this formula to transform it into a trigonometric form:

`\boxedz`

We substitute the values already obtained:

`\boxed{ \bold{z \: = \: 5 * \: ( \cos( 53.13°) \: + \: i \: * \: \sin( 53.13°))}}`

Answer:

`\boxed{ \bold{z \: = \: 5 * \: ( \cos( 53.13°) \: + \: i \: * \: \sin( 53.13°))}}`

MissSpanish