Answer: Choice B
h(c) = 1 for at least one c between -3 and 4
====================================================
Step-by-step explanation:
Draw an xy axis system. Plot the points (-3,-1) and (4,2) on this grid. These points come from the fact that h(-3) = -1 and h(4) = 2. These are the endpoints of the h(x) function.
Next, draw horizontal lines through both points. Also, draw vertical lines through the two points as well. A rectangle will form.
The region inside this rectangle is all we care about.
We're told that h(x) has endpoints mentioned earlier, and h(x) is continuous, so that means we have some curve or line through the two points. One such example is shown below. There are infinitely many possible curves to draw out as long as they stay in the rectangle.
----------------------
After you have your h(x) function curve drawn, draw a horizontal line through y = 1 on the y axis. This is the dashed line in the diagram below.
This horizontal line crosses the green h(x) curve at one point or more. In my example, it does so at one point only. However, you could easily draw h(x) so that it crosses y = 1 as many times as you want (just have it squiggle up and down multiple times).
This shows that h(c) = 1 is possible when
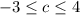. Here c is playing the role of x since it is the input of a function. The h(c) is the output, so that's the y value.
This says that for some input between -3 and 4, it's possible to get an output of 1.
-------------------------
Here's a real world example of the intermediate value theorem.
Let's say the endpoints are A and B, and they are two towns.
The h(x) curve is a road connecting the towns.
To go from A to B, or vice versa, we need to cross over some border that is between the towns. The border in this case is the dashed horizontal line in the diagram.
side note: A special use of the intermediate value theorem is to show that a root exists on some interval (if you know the function changes between positive to negative, or vice versa).