1 Answer

Amillerrhodes · Answer 1 · 2023-06-14T19:30:29+0000

Convert to polar coordinates with

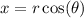
$x = r \cos(\theta)$

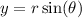
$y = r \sin(\theta)$

so that
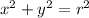x^2 + y^2 = r^2 , and the Jacobian determinant for this change of variables is

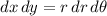
$dx\,dy = r \, dr \, d\theta$

D is the disk centered at the origin with radius 2; in polar coordinates, this is the set

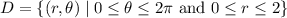
$D = \left\{(r, \theta) \mid 0\le\theta\le2\pi \text{ and } 0 \le r \le 2\right\}$

Then the integral is

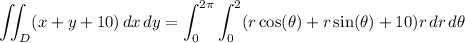
$\displaystyle \iint_D (x + y + 10) \, dx \, dy = \int_0^(2\pi) \int_0^2 (r \cos(\theta) + r \sin(\theta) + 10) r \, dr \, d\theta$

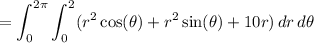
$\displaystyle = \int_0^(2\pi) \int_0^2 (r^2 \cos(\theta) + r^2 \sin(\theta) + 10r) \, dr \, d\theta$

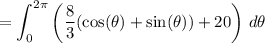
$\displaystyle = \int_0^(2\pi) \left(\frac83 (\cos(\theta) + \sin(\theta)) + 20\right) \, d\theta$

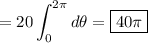
$\displaystyle = 20 \int_0^(2\pi) d\theta = \boxed{40\pi}$

(since cos and sin are 2π-periodic)

Please log in or register to add a comment.