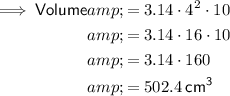Question

b solve each problem . use ñ= 3.14 1. what is the volume of a regular cylinder whose base has radius of 5 cm and has height of 4 cm? 2. the diameter of sphere is 10 cm. find the volume. 3. juice is sold in aluminum cans that measure 7 inches in height and 4 inches in diameter. how many cubic inches of juice are contained in a full can? 4. the square pyramid has a volume of 297 cm³. the area of the base is 81 cm². What is the height.? 5. A glass is 10 cm deep and 8 cm wide . How much liquid the glass hold?​

Answer 1

#1

Volume

• πr²h
• π(5)²(4)
• 100π
• 3.14(100)
• 314cm³

#2

Radius=10/2=5cm

Volume

• 4/3πr³
• 4/3π(5)³
• 125(4/3π)
• 500π/3
• 523.3cm³

#3

Volume

• π(4/2)²(7)
• 2²(7π)
• 28π
• 87.92in³

#4

• V=1/3a²h
• V=1/3(81)h
• 27h=297
• h=11cm

#5

radius=8/2=4

Volume

• π(4)²(10)
• 160π
• 502.4cm³
• 502.4mL

Answer 2

1) 314 cm³

2) 523.33 cm³

3) 87.92 in³

4) 11 cm

5) 502.4 cm³

Explanation:

Part 1

`\textsf{Volume of a cylinder}=\sf \pi r^2 h \quad\textsf{(where r is the radius and h is the height)}`

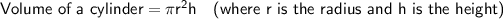
Given:

• r = 5 cm
• h = 4 cm
• π = 3.14

Substitute the given values into the formula:

`\begin{aligned}\implies \textsf{Volume} & =3.14 \cdot 5^2 \cdot 4\\& = 3.14 \cdot 25 \cdot 4\\& = 3.14 \cdot 100\\& = 314 \: \sf cm^3\end{aligned}`

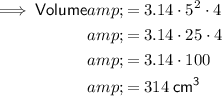
Part 2

`\textsf{Volume of a sphere}=\sf \frac43 \pi r^3\quad\textsf{(where r is the radius)}`

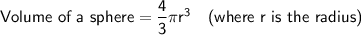
Given:

• d = 10 cm ⇒ r = 5 cm
• π = 3.14

Substitute the given values into the formula:

`\begin{aligned}\implies \textsf{Volume} & =(4)/(3) \cdot 3.14 \cdot 5^3 \\& =(4)/(3) \cdot 3.14 \cdot 125 \\& =(500)/(3) \cdot 3.14 \\& = 523.33\: \sf cm^3\:(2\:dp)\end{aligned}`

Part 3

`\textsf{Volume of a cylinder}=\sf \pi r^2 h \quad\textsf{(where r is the radius and h is the height)}`

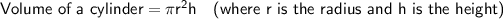
Given:

• d = 4 in ⇒ r = 2 in
• h = 7 in
• π = 3.14

Substitute the given values into the formula:

`\begin{aligned}\implies \textsf{Volume} & =3.14 \cdot 2^2 \cdot 7\\& = 3.14 \cdot 4 \cdot 7\\& = 3.14 \cdot 28\\& = 87.92\: \sf in^3\end{aligned}`

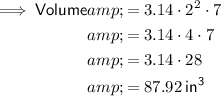
Part 4

`\textsf{Volume of a square pyramid}=\sf (1)/(3) a^2h \quad\textsf{(where a is the base edge and h is the height)}`
`\textsf{Area of base of square pyramid}=\sf a^2 \quad\textsf{(where a is the base edge)}`

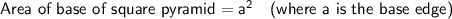
Given:

• Volume = 297 cm³
• Area of base = 81 cm²

`\implies 81=a^2`

`\implies a=√(81)`

`\implies a=9\: \sf cm`

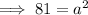
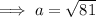
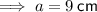
Substitute the given values into the formula and solve for h:

`\begin{aligned}\implies \textsf{297} & =(1)/(3) \cdot 9^2 \cdot h\\\\297 & =(81)/(3) h\\\\891 & =81 h\\\\h & = 11 \: \sf cm\end{aligned}`

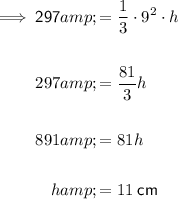
Part 5

`\textsf{Volume of a cylinder}=\sf \pi r^2 h \quad\textsf{(where r is the radius and h is the height)}`

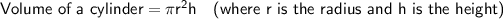
Given:

• d = 8 cm ⇒ r = 4 cm
• h = 10 cm
• π = 3.14

Substitute the given values into the formula:

`\begin{aligned}\implies \textsf{Volume} & =3.14 \cdot 4^2 \cdot 10\\& = 3.14 \cdot 16 \cdot 10\\& = 3.14 \cdot 160\\& = 502.4\: \sf cm^3\end{aligned}`