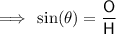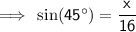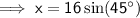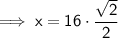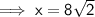Answer:
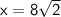
Explanation:
Trigonometric ratios
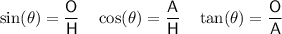
where:
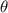 is the angle
is the angle- O is the side opposite the angle
- A is the side adjacent the angle
- H is the hypotenuse (the side opposite the right angle)
Therefore, to find x we need to use the sine trig ratio.
Given:
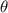 = 45°
= 45°- O = x
- H = 16
Substitute these values into the formula and solve for x: