Question

Write the domain and range of the function as an inequality

Answer 1

Answer: Choice C

Domain =
`-\infty < x < +\infty`

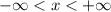
Range =
`y \le -4`

======================================

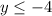
Step-by-step explanation:

The arrows on the graph indicate it goes on forever in both left and right directions. So the domain is the set of all real numbers and as an inequality, we write
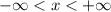`-\infty < x < +\infty` which is the same as saying
`-\infty < x < \infty`

This says x is between negative infinity and positive infinity.

In set builder notation, we would say
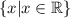`\{x | x \in \mathbb{R}\}` and in interval notation, we would write
`(-\infty, \infty)`

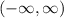
As you can probably see, the domain is the set of all possible x inputs of a function.

--------------------------

The range is the set of all possible y outputs of a function.

The largest output is y = -4 which is where the vertex is located.

There is no smallest y value as the arrows point down, and the graph goes forever in that direction.

So we say the range is
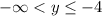`-\infty < y \le -4` which shortens to
`y \le -4`

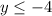
The range in set builder notation is
`\{y | y \in \mathbb{R}, \ y \le -4\}`

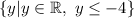
The range in interval notation is
`(-\infty, -4]` The square bracket says to include the endpoint, while the parenthesis excludes the endpoint.