Answer:
Option (C)
Explanation:
In this question we will use the property " similarity of the triangles".
If DE and AC are parallel two triangles BED and BCA will be similar, corresponding sides of the triangles will be proportional.
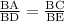
Option (A).
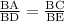
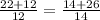
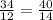
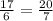
But
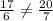
Therefore, given triangles are not similar.
AC and DE are not parallel.
Option (B).
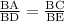
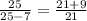
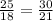
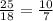
But
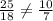
Therefore, AC and DE are not parallel.
Option (C).
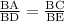
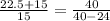
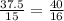
2.5 = 2.5
Therefore, AC║DE.
Option (D).
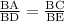
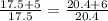
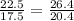
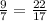
But
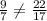
Therefore, AC and DE are not parallel.
Option (C) will be the answer.