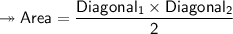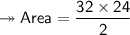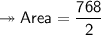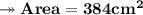Given :
- Diagonal_1 of rhombus = 24 cm

To find :

Note :
Kindly keep in touch with picture

Solution:
We know:

As we can clearly see we need both diagonals, but in question only one diagonal is given.

So first let's find other diagonal.

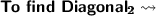

In △ AOB :
AB - Hypotenuse
AO = Perpendicular
BO = Base

Base² = Hypotenuse ² - Perpendicular²
∴ BO² = AB² - AO²
- BO² = 20² - 12²
- BO² = 400 - 12²
- BO² = 400 - 144
- BO² = 256
- BO = √(256)
- BO = √(16 × 16)
- BO = 16 cm²

- Diagonal_2 = 2BO
- Diagonal_2 = 2 × 16
- Diagonal_2 = 32 cm

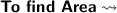

As we already know Area of rhombus so :