Answer:
Option (D)
Explanation:
If a point (h, k) divides the line segment having ends at
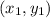 and
and
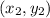 in the ratio of m : n then,
in the ratio of m : n then,
h =
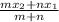
k =
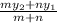
If a point Q(h, k) divides the segment with ends A(-4, 6) and B(6, 1) in the ratio of 3 : 2 then,
h =
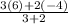
=
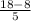
h = 2
k =
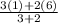
=
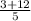
k = 3
Therefore, Coordinates of the point Q are (2, 3).
Option (D) will be the answer.