Question

3x - 2y < -5

x + 4y > 8
The solution set to the system of inequalities is graphed. What is wrong with the graph? A) The wrong region is shaded.
B) One line has the wrong slope.
C) Nothing, the graph is correct.
D) One line has the wrong y-intercept.

Answer 1

Answer: A. The wrong region is shaded

Explanation:

Let's solve for y in the first equation.

3x−2y<−5

Step 1: Add -3x to both sides.

3x−2y+−3x<−5+−3x

−2y<−3x−5

Step 2: Divide both sides by -2.

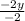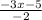
`(-2y)/(-2)`<
`(-3x-5)/(-2)`

y >
`(3)/(2)x+(5)/(2)`

graph the equation using the slope
`(3)/(2)` and the y-intercept
`(5)/(2)`

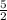
The line is dotted because it is > (not ≥)

shade in the left side by plugging in (0,0) into x and y and finding

0 is not > than
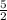`(5)/(2)`. This means you shade in the side not include the origin.

Do this same thing for the next equation.

Let's solve for y in the second equation.

x+4y>8

Step 1: Add -x to both sides.

x+4y+−x>8+−x

4y>−x+8

Step 2: Divide both sides by 4.

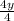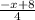
`(4y)/(4)` >
`(-x+8)/(4)`

y >
`(-1)/(4)x+2`

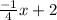
graph the equation using the slope
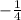`-(1)/(4)` and the y-intercept 2

(Dotted line), (plug in 0,0 and find 0 is not > than 2. So shade the region not including the origin (0,0).

Hope this helps.