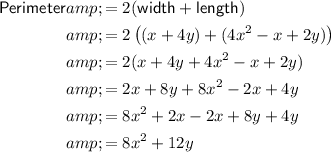Answer:
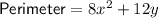
Explanation:
A rectangle has 2 pairs of parallel, congruent sides.
The perimeter of a two-dimensional shape is the distance all the way around the outside. Therefore, the perimeter of a rectangle is twice the sum of its length and width.
Given:
- width =
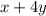
- length =
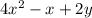
Therefore: