Question

2. Consider the following points.

A(-2,20) and P (10,-13)
AP undergoes the translation Tox(x,y), such that A (-28, 37) and P'(-16,4).
Part A: Complete the following algebraic description.
b
(x,y) → (x +
x= x
Part B: Which of the following statements is true?
A AP and A'P' have different locations.
B AP and A'P' have different shapes.
CAP and A'P' have different sizes.
D AP and A'P' have different directions.

Answer 1

Transformation: (x,y) → (x - 26, y + 17) or

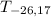`T _(-26,17)`(x,y) [translation]

A, since the transformation of a translation simply changes the location of a certain figure because all the points of the figure are moved the exact same way. This is because a translation is a rigid transformation.

Step-by-step explanation:

Let the preimage of points A and P be A(x1,y1), and P(x2,y2). And the image of points A and P be A'(x3,y3) and P'(x4,y4).

Given points A and P are A(-2,20) and (10,-13). And points A' and P' are A'(-28,37), and P'(-16,4). The translation is found by calculating the difference between these points for the figure. (x,y) → (( x + ((x3-x1) + (x4-x2))/2), (y + ((y3-y1) + (y4-y2))/2 )). If this does not match all the points in the transformation of the figure, than it is not a rigid transformation, and so it cannot be a translation.

The simple formula for the uniform translation of a figure is : (x,y) → ((x + (x2-x1), (y + (y2-y1)) . Where x2, and y2 are part of the image, while x1, and y1 are part of the preimage. This will get you from the preimage(1) to image(2) following a translation.

Given all the points, the more complicated work is shown here:

(x,y) → ((x + ((-28--2) + (-16-10))/2), (y + ((37-20) + (4--13))/2)) = (x,y) → ((x + (-26 + -26)/2),(y + (17 + 17)/2) = (x,y) → ((x - 26),(y + 17)) = (x,y) → (x - 26, y + 17).

When writing a transformation like a translation in a function, it will look like this:
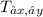`T _(∆x,∆y)`(x,y). ∆x,∆y are just placeholders for the change in these variables that get you from the preimage to image.