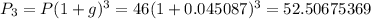Question

You are considering an investment in Justus Corporation’s stock, which is expected to pay a dividend of $2.25 a share at the end of the year (D1 = $2.25) and has a beta of 0.9. The risk-free rate is 4.9%, and the market risk premium is 5%. Justus currently sells for $46.00 a share, and its dividend is expected to grow at some constant rate, g. Assuming the market is in equilibrium, what does the market believe will be the stock price at the end of 3 years? (That is, what is P3 ?)

Answer 1

The price 3-years from now will be of $52,50

Step-by-step explanation:

We solve for g using the Gordon model:

`(divends(1+g))/(Price) = return-growth`

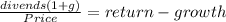
As we don't know the rate of return we solve ofr that fist using CAPM:

CAPM (Capital Assets Price Model)

`Ke= r_f + \beta (r_m-r_f)`

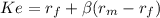
risk free 0.049

market rate 0.099

premium market = market rate - risk free 0.05

beta(non diversifiable risk) 0.9

`Ke= 0.049 + 0.9 (0.05)`

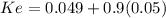
Ke 0.09400

We plug that in the gordon equation and solve for g:

`(2.25)/(Price) = return-growth`

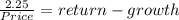
2.25 = 0.094 x 46 - g x 46

(2.25 - 4.324) / 46 = -g

-0.0450869565217391 = -g

g = 0.045087

In the gordon model the price of the stock increases at the grow rate:

as P = D/(r-g)

P1 = D(1+g)/r-g)

P1 / P = D(1+g)/(r- g) / D/(r- g) = 1 + g

`P_3 = P(1+g)^3 = 46(1+0.045087)^3 = 52.50675369`