Question

Question 1 (2 points)

(03.04)

For the function f(x) = -(x + 1)2 + 4, identify the vertex, domain, and range. (2 points)

A-The vertex is (-1,4), the domain is all real numbers, and the range is y greater than4.

B-The vertex is (-1, 4), the domain is all real numbers, and the range is y less than4.

C-The vertex is (1,4), the domain is all real numbers, and the range is y greater than 4.

D-The vertex is (1.4), the domain is all real numbers, and the range is y less than4.

Answer 1

The vertex is (-1, 4), the domain is all real numbers, and the range is y less than 4

Explanation:

Given

`f(x) = -(x+1)^2 + 4`

Solving (a): The vertex;

Assume the general form of a function is

`f(x) = a(x-h)^2+k`

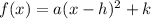
The vertex is determined by
`(h,k)`

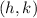
By comparison, we have:

`-h = 1`

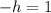
Solve for h, we have:

`h = -1`

`k = 4`

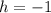
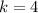
So, the vertex is:

`(h,k) = (-1,4)`

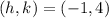
The domain; x is all real numbers

From the function;

`f(x) = -(x+1)^2 + 4`

This can be rewritten as:

`f(x) = 4 - (x+1)^2`

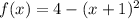
This implies that:

Whatever the value of
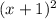`(x + 1)^2` is, it will be subtracted from 4 to give y or f(x);

Hence:

y is less than 4

Option B answers the question