Answer:
The period of that same pendulum on the moon is 12.0 seconds.
Step-by-step explanation:
To determine the period of that same pendulum on the moon,
First, we will determine the value of g (which is a measure of the strength of Earth's gravity) on the Moon. Let the value of g on the Moon be
 .
.
From the question, the strength of earth’s gravity is only 1/6th of the normal value. The normal value of g is 9.8 m/s²
∴
 =
=
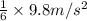
 = 1.63 m/s²
= 1.63 m/s²
From the question, T=2π√L/g
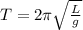
We can write that,
 .......... (1)
.......... (1)
Where
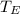 is the period of the pendulum on Earth and
is the period of the pendulum on Earth and
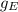 is the measure of the strength of Earth's gravity
is the measure of the strength of Earth's gravity
and
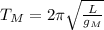 .......... (2)
.......... (2)
Where
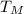 is the period of the pendulum on Moon and
is the period of the pendulum on Moon and
 is the measure of the strength of Earth's gravity on the Moon.
is the measure of the strength of Earth's gravity on the Moon.
Since we are to determine the period of the same pendulum on the moon, then,
 and
and
 are constants.
are constants.
Dividing equation (1) by (2), we get
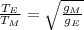
From the question,
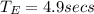
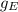 = 9.8 m/s²
= 9.8 m/s²
 = 1.63 m/s²
= 1.63 m/s²
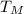 = ??
= ??
From,
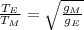
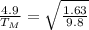
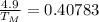
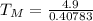
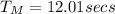
∴
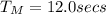
Hence, the period of that same pendulum on the moon is 12.0 seconds.