Question

Question 1: The director of a green energy company is interested in comparing two different methods of installing solar light panels. An experiment is conducted with 31 technicians using the old method and the other 46 technicians using the new method. For the 31 technicians using the old method, the average time was 525 minutes with 47.7 standard deviation. For the 46 technicians using the new method, the average time was 520 minutes with 48.2 standard deviation. Conduct an analysis to determine whether there is a difference in the average time to complete the installation of the solar panels. Provide the test statistic value.

Question 2:

The director of a green energy company is interested in comparing two different methods of installing solar light panels. An experiment is conducted with 39 technicians using the old method and the other 55 technicians using the new method.

For the 39 technicians using the old method, the average time was 582 minutes with 63.8 standard deviation.
For the 55 technicians using the new method, the average time was 542 minutes with 97.8 standard deviation.
Conduct an analysis to determine whether there is a difference in the average time to complete the installation of the solar panels. Provide the degrees of freedom.

Answer 1

Question 1

The test statistics is
`t = 0.44`

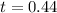
The decision rule is

Fail to reject the null hypothesis

The conclusion

There is no sufficient evidence to show that there is a difference in the average time to complete the installation of the solar panels

Question 2

The degree of freedom is
`df = 92`

The decision rule is

Reject the null hypothesis

The conclusion

There is sufficient evidence to show that there is a difference in the average time to complete the installation of the solar panels

Step-by-step explanation:

Considering Question 1

Here we are told to provide the test statistics

From the question we are told that

The first sample size is
`n_1 = 31`

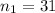
The second sample size is
`n_ 2 =  46`

The first sample mean is
`\= x_1 = 525 \ minutes`

The first standard deviation is
`\sigma_1 =  47.7`

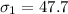
The second sample mean is
`\= x_2 = 520 \ minutes`

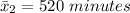
The second standard deviation is
`\sigma_2 =  48.2`

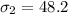
The null hypothesis is
`H_o :  \mu_1 - \mu_2 = 0`

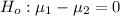
The alternative hypothesis is
`H_a :  \mu_1 - \mu_2 \\e 0`

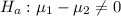
Generally the degree of freedom is mathematically represented as

`df = n_1 + n_2  -2`

=>
`df = 31 + 46  -2`

=>
`df = 75`

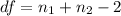
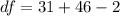
Generally the test statistics is mathematically represented as

`t =  \frac{(\= x_1 - \= x_2 )-0}{ \sqrt{(\sigma_1^2)/(n_1) + (\sigma_2^2)/(n_2) } }`

=>
`t =  \frac{( 525-  520 )-0}{ \sqrt{(47.7^2)/(31) + (48.2^2)/(46) } }`

=>
`t = 0.44`

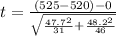
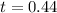
Let assume that the level of confidence is
`\alpha = 0.05`

Generally the probability of t at a degree of freedom of is
`df = 75`

`P(t > 0.44 ) = 0.33060124`

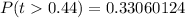
Generally the p-value is mathematically represented as

`p-value  =  2 *  P(t > 2.398)`

=>
`p-value  =   2 * 0.33060124`

=>
`p-value  =  0.66120`

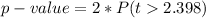
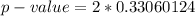
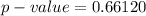
From the value obtain we see that
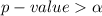`p-value  >  \alpha` hence we fail to reject the null hypothesis

The conclusion is that there is no sufficient evidence to show that there is a difference in the average time to complete the installation of the solar panels

Considering Question 2

Here we are told to provide the degree of freedom

From the question we are told

The first sample size is
`n_1 = 39`

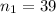
The first sample mean is
`\= x_1 = 582 \ minutes`

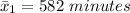
The first standard deviation is
`\sigma_2 =  63.8`

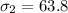
The second sample size is
`n_ 2 =  55`

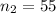
The second sample mean is
`\= x_2 = 542 \ minutes`

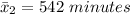
The second standard deviation is
`\sigma_2 =  97.8`

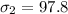
The null hypothesis is
`H_o :  \mu_1 - \mu_2 = 0`

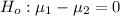
The alternative hypothesis is
`H_a :  \mu_1 - \mu_2 \\e 0`

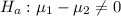
Generally the degree of freedom is mathematically represented as

`df = n_1 + n_2  -2`

=>
`df = 39 + 55  -2`

=>
`df = 92`

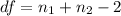
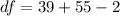
Generally the test statistics is mathematically represented as

`t =  \frac{(\= x_1 - \= x_2 )-0}{ \sqrt{(\sigma_1^2)/(n_1) + (\sigma_2^2)/(n_2) } }`

=>
`t =  \frac{( 582 -  542 )-0}{ \sqrt{(63.8^2)/(39) + (97.8^2)/(55) } }`

=>
`t = 2.398`

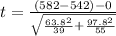
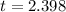
Let assume that the level of confidence is
`\alpha = 0.05`

Generally the probability of t at a degree of freedom of is
`df = 92`

`P(t > 2.398 ) = 0.00925214`

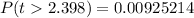
Generally the p-value is mathematically represented as

`p-value  =  2 *  P(t > 2.398)`

=>
`p-value  =   2 * 0.00925214`

=>
`p-value  =  0.0185`

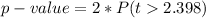
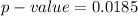
From the value obtain we see that
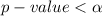`p-value  <  \alpha` hence we reject the null hypothesis

The conclusion is that there is sufficient evidence to show that there is a difference in the average time to complete the installation of the solar panels