Answer:
Step-by-step explanation:
From the given information;
The first objective is to derive an expression for the execution time in cycles
For an execution time T for the non-pipelined processor;
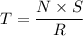
where
N = instruction count
S = average number of clock cycles to fetch & execute an instruction
R = clock rate
From the average number of clock
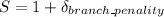
where;
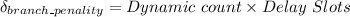
Similarly, we are given that the dynamic count is 20%
∴
The execution time required for all the delayed slots that is filled with NOP instructions can be estimated as:
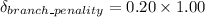
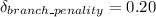
Therefore;
S = 1 + 0.20
S = 1.2
Recall that:
For an execution time T for the non-pipelined processor;
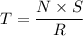
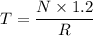
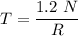
To derive another expression that reflects the execution time of 70% delay; we have:
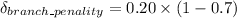
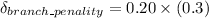
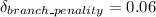
S = 1 + 0.06
S = 1.06
For an execution time T for the non-pipelined processor;
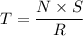
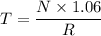
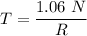
Finally, the compiler's contribution to the increase in speed up percentage for the above two cases is:
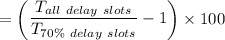
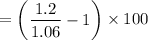
= (1.1320 - 1) × 100
= 0.1320 × 100
= 13.20%
Therefore, the compiler's contribution to increasing performance as expressed as speed up percentage is 13.20%