The given dimensions of the base of the box are 2 x 3 units.
Let h be the height of the box.
So, the volume of the box = 2 x 3 x h ...(i)
The shape of baseball is spherical and one baseball fits in a cubical box having the minimum dimensions equal to the diameter of the spherical ball.
Assuming the diameter of the baseball is d units.
So, the volume occupied by one baseball= volume of the cubical box having the side
 units.
units.
 cubic units
cubic units
So, the volume required to pack 48 baseballs
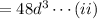
Assuming that all the baseballs fit in the box, i.e peripheral balls in every horizontal and vertical layer touched the box as shown in the figure.
So, the length, 3 units and the width, 2 units, must be the integral multiple of the diameter,
 units, of the baseball. i.e
units, of the baseball. i.e
The length,
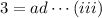
The width,
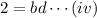
The height,

where
 and
and
 belong to the natural number.
belong to the natural number.
This required volume must be equals to the volume of the box.
From equations (i) and (ii),
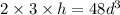
[from (iii) and (iv)]

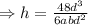
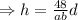
On comparing with the equation (iv)
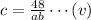
Now, if the diameter of the baseball is unity,i.e, d=1 unit
( integer) and (integer) [from (iii) and (iv)]
(also an integer) [from (v)]
Now, the height of the box,
 unit.
unit.
Hence, the other dimension of the box, is 8 units corrosponding to the unity diameter of the baseball.
Note the height of the box depends on the diameter of the baseball, so it will have infinite possible value for different value of the diameter.
For example, the value of height for d=1 unit has been shown.
and another example may be if units, then (integer) and (integer)
(also an integer) [from (v)]
Now, the height of the box,
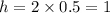 unit. [from (iv)]
unit. [from (iv)]
Here, the height of the box is 2 units corrosponding to 0.5 unit diameter of the baseball.
The possivle values of d can be taken for which
 and
and
 must be integers.
must be integers.