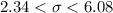Answer:
a
The confidence interval for the population variance is
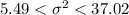
The correct option is C
b
The confidence interval for the population standard deviation is
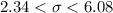
The correct option is A
Explanation:
From the question we are told that
The sample size is n = 14
The standard deviation is
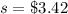
Generally the degree of freedom is mathematically represented as
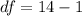
=>
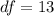
Given that the confidence level is 98% then that level of significance is
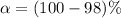
=>
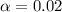
Generally the 98% confidence interval for the variance is mathematically represented as
![\frac{(n- 1) s^2}{x^2 _{[(\alpha )/(2) , df]}} < \sigma^2 < \frac{(n- 1) s^2}{x^2 _{[1- (\alpha )/(2) , df]}}](https://img.qammunity.org/2021/formulas/mathematics/college/qmkywuxf0npmhj9ph6dr3tqrh2cq9bz0ib.png)
=>
![\frac{(14- 1) (3.42)^2}{x^2 _{[(0.02 )/(2) , 13]}} < \sigma^2 < \frac{(14- 1) (3.42)^2}{x^2 _{[1- (0.02 )/(2) , 13]}}](https://img.qammunity.org/2021/formulas/mathematics/college/2e4dd0an0jiw6fgxzj40szp1rsx5qzma0j.png)
From the chi -distribution table
![x^2 _{[1- (0.02 )/(2) , 13]} = 4.107](https://img.qammunity.org/2021/formulas/mathematics/college/an0cjj7hwawa4udq96zhlcjgl1lo5cw1vp.png)
and
![x^2 _{[(0.02 )/(2) , 13]} = 27.689](https://img.qammunity.org/2021/formulas/mathematics/college/suq9eqa0814n88ugvh8mf2j7dxtq7fmuel.png)
So
=>
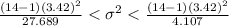
=>
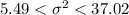
Generally the 98% confidence interval for the standard deviation is mathematically represented as
![\sqrt{\frac{(n- 1) s^2}{x^2 _{[(\alpha )/(2) , df]}}} < \sigma <\sqrt{ \frac{(n- 1) s^2}{x^2 _{[1- (\alpha )/(2) , df]}}}](https://img.qammunity.org/2021/formulas/mathematics/college/8phzdr7jda0dv1r49o5sffzjh8mrokdx5w.png)
=>
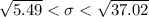
=>