Question

The height h in feet of an object t seconds after it is dropped can be modeled by the quadratic equation h=-16t^2+h0, where h0 is the initial height of the object. Solve the equation h=-16t^2+255 for t, using the quadratic formula to determine the time it takes the rock to reach the canyon floor.

Answer 1

The rock will take approximately 3.992 seconds to reach the canyon floor.

Explanation:

For all
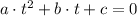`a\cdot t^(2)+b\cdot t + c = 0`, its roots are determined by the Quadratic Formula:

`t = \frac{-b\pm\sqrt{b^(2)-4\cdot a\cdot c}}{2\cdot a}`

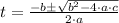
In this case, it corresponds to instants when rock is either launched or hits the floor. If we know that
`a = -16`,
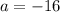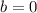`b = 0` and
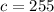`c = 255`, the time it takes the rock to reach the canyon floor is:

`t = \frac{-0\pm\sqrt{(0)^(2)-4\cdot (-16)\cdot (255)}}{2\cdot (-16)}`

`t \approx 3.992\,s`

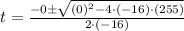
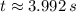
The rock will take approximately 3.992 seconds to reach the canyon floor.