Answer:
45 minutes
Explanation:
Let, after time
 minutes, they meet again at the same point.
minutes, they meet again at the same point.
In time
 minutes, let Sony completes x lap while Iogan completes y laps. Note that x and y must be the counting numbers.
minutes, let Sony completes x lap while Iogan completes y laps. Note that x and y must be the counting numbers.
As Sonny took 15 minutes to drive 1 lap, so,

While Iogan Sonny took 9 minutes to drive 1 lap, so,

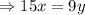 [from equation (i)]
[from equation (i)]

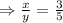
As x,y must be counting number, so
(x,y)=(3,5),(6,10),...,(3n,5n) where n is a positive integer.
So, the minimum number of laps required are
x=3 and y=5 (when they meet for the first time)
Now, from equation (i),
The time required to meet them for the first time, t=15x3=45 minutes.