Answer:
Power = 124.50 W
Step-by-step explanation:
Given that:
The Sound intensity of a speaker output is 102 dB
and the distance r = 25 m
For the intensity of sound,
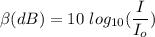
where;
the threshold of hearing
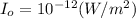
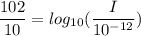
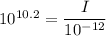
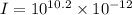
I = 0.01585 W/m²
If we recall, we know remember that ;
Power = Intensity × A rea
Power = 0.01585 W/m² × 4 × 3.142 × (25 m)²
Power = 124.50 W