Question

If a power utility were able to replace an existing 500 kV transmission line with one operating at 1 MV, it would change the amount of heat produced in the transmission line to

Answer 1

It would change the amount of heat produced in the transmission line to four times the previous value.

Step-by-step explanation:

Given;

initial voltage in the transmission line, V₁ = 500 kV = 500,000 V

Final voltage in the transmission line, V₂ = 1 MV = 1,000,000

The power lost in the transmission line due to heat is given by;

`P = (V^2)/(R)`

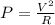
Power lost in the first wire;

`P_1 = (V_1^2)/(R)`

`R = (V_1^2)/(P_1)`

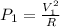
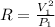
Power lost in the second wire

`P_2 = (V_2^2)/(R)\\\\ R = (V_2^2)/(P_2)`

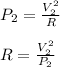
Keeping the resistance constant, we will have the following equation;

`(V_2^2)/(P_2) = (V_1^2)/(P_1) \\\\P_2 = (V_2^2P_1)/(V_1^2)\\\\`

`P_2 = ((1,000,000)^2P_1)/((500,000)^2)\\\\P_2 =4P_1`

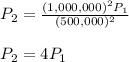
Therefore, it would change the amount of heat produced in the transmission line to four times the previous value.