Question

Calculate the effective value of g, the acceleration of gravity, at 6700 m , above the Earth's surface. g

Answer 1

The effective value of g at 6700 m above the Earth's surface is 9.79 m/s².

Step-by-step explanation:

The value of g can be found using the following equation:

`F = (GmM)/(r^(2))`

`ma = (GmM)/(r^(2))`

`a = (GM)/(r^(2))`

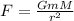
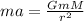
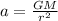
Where:

a is the acceleration of gravity = g

G: is the gravitational constant = 6.67x10⁻¹¹ m³/(kg.s²)

M: is the Earth's mass = 5.97x10²⁴ kg

r: is the Earth's radius = 6371 km

Since we need to find g at 6700 m, the total distance is:

`r_(T) = 6371000 m + 6700 m = 6377700 m`

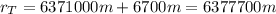
Now, the value of g is:

`a = (GM)/(r_(T)^(2)) = (6.67\cdot 10^(-11) m^(3)/(kg*s^(2))*5.97 \cdot 10^(24) kg)/((6377700 m)^(2)) = 9.79 m/s^(2)`

Therefore, the effective value of g at 6700 m above the Earth's surface is 9.79 m/s².

I hope it helps you!