Question

A cup of hot coffee initially at 95 degrees C cools to 80 degrees C in 5 min while sitting in a room of temperature 21 degrees C. Using Newton's law of cooling, determine when the temperature of the coffee will be a nice 50 degrees C.

Answer 1

When the temperature of the coffee is 50 °C, the time will be 20.68 mins

Step-by-step explanation:

Given;

The initial temperature of the coffee T₀ = 95 °C

The temperature of the room = 21°C

Let T be the temperature at time of cooling t in mins

According to Newton's law of cooling;

`(dT)/(dt) \alpha (T-21)\\\\(dT)/(dt) = k (T-21)\\\\(dT)/(T-21) = kdt\\\\\int\limits {(dT)/(T-21)} = \int\limits kdt\\\\Log(T-21) =kt + Logc \\\\Log ((T-21)/(c) ) = kt\\\\T -21 = ce^(kt)\\\\At \ t = 0, T = 95\\\\95-21 = ce^0\\\\74 = c\\\\New, equation: T -21 = 74e^(kt)\\\\Again; when \ t= 5\ min, T = 80\\\\80 -21 = 74e^(5k)\\\\59 = 74e^(5k)\\\\e^(5k) = (59)/(74)\\\\ 5k = ln((59)/(74))\\\\5k = -0.2265\\\\k = -0.0453`

When the temperature is 50 °C, the time t in min is calculated as;

`T -21 = 74e^(-0.0453t)\\\\50 -21 = 74e^(-0.0453t)\\\\29 = 74e^(-0.0453t)\\\\(29)/(74) = e^(-0.0453t)\\\\0.39189 = e^(-0.0453t)\\\\ln(0.39189 ) = {-0.0453t}\\\\-0.93677 = {-0.0453t}\\\\t = (-0.93677)/(-0.0453)\\\\ t = 20.68 \ mins`

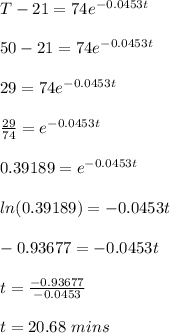
Therefore, when the temperature of the coffee is 50 °C, the time will be 20.68 mins