Answer:
The energy contained is 5.856 x 10⁻⁶ J
Step-by-step explanation:
Average energy density of electromagnetic radiation per unit volume is given by the equation;
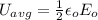 ²
²
where;
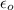 is permittivity of free space
is permittivity of free space
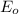 is maximum electric field strength, this can be calculated from the intensity of sun reaching the Earth's surface.
is maximum electric field strength, this can be calculated from the intensity of sun reaching the Earth's surface.
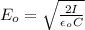
The intensity of sun reaching the Earth is 1350 W/m²
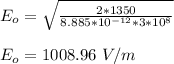
Average energy density of electromagnetic radiation per unit volume;
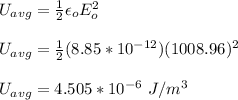
The energy contained in a 1.30 m³ volume is given by;
E = (4.505 x 10⁻⁶)(1.3)
E = 5.856 x 10⁻⁶ J
Therefore, the energy contained is 5.856 x 10⁻⁶ J