Question

A certain liquid has a normal boiling point of and a boiling point elevation constant . A solution is prepared by dissolving some potassium bromide () in of . This solution boils at . Calculate the mass of that was dissolved.

Answer 1

`m_(KBr)=6.030gKBr`

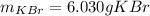
Step-by-step explanation:

Hello.

In this case, since the normal boiling point of X is 117.80 °C, the boiling point elevation constant is 1.48 °C*kg*mol⁻¹, the mass of X is 100 g and the boiling point of the mixture of X and KBr boils at 119.3 °C, we can use the following formula:

`(T_b-T_b_0)=i*m*K_b`

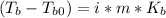
Whereas the Van't Hoff factor of KBr is 2 as it dissociates into potassium cations and bromide ions; it means that we can compute the molality of the solution:

`m=(T_b-T_b_0)/(i*K_b)=((119.3-117.8)\°C)/(2*1.48\°C*kg*mol^(-1))\\ \\m=0.507mol/kg`

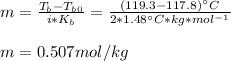
Next, given the mass of solventin kg (0.1 kg from 100 g), we compute the moles KBr:

`n_(KBr)=0.507mol/kg*0.1kg=0.0507mol`

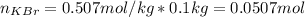
Finally, considering the molar mass of KBr (119 g/mol) we compute the mass that was dissolved:

`m_(KBr)=0.0507mol*(119g)/(1mol) \\\\m_(KBr)=6.030gKBr`

Best regards.