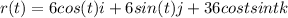Complete Question
find a vector function that represents the curve of intersection of the two surfaces. The cylinder
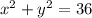 an the surface
an the surface

Answer:
The function is

Explanation:
From the question we are told that
The equation of the cylinder is
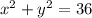
The equation of the surface is z = xy
Generally the general form of this function is

Generally to confirm the RHS and the LHS of the equation for the cylinder
Let take x (t) = 6cos(t)
and y(t) = 6sin (t)
So
![x^2 + y^2 = [ 6cos(t)]^2 + [6 sin (t)]^2](https://img.qammunity.org/2021/formulas/mathematics/college/4r2i10nj08rxjkz4pd9f0hl4qqy13d8mac.png)
=>
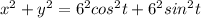
=>
![x^2 + y^2 = 6^2 [cos^2t + sin ^2t]](https://img.qammunity.org/2021/formulas/mathematics/college/wo6vzsulyamsxd6vt2gxoeuf7khfoglbwe.png)
Generally
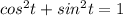
So

So at x (t) = 6cos(t) and y(t) = 6sin (t) the RHS is equal to LHS
So
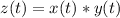
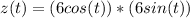
=>
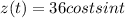
So the function is