Answer:
a
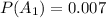
b
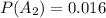
c
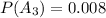
d
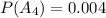
e

Explanation:
From the question we are told that
The number of cards selected is n = 7
Generally in a standard deck of cards
The total number of cards is N = 52
The number of hearts is h = 13
The number of diamonds is d = 13
The number of spade is s = 13
The number of Ace is a = 4
The number of kings is k = 4
Considering question a
The number of ways to selected 5 hearts out of the 13 hearts is mathematically represented as
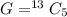
Here C means combination so
The number of cards that is not hearts is 52 - 13 = 39
Generally the number of ways of selecting the reaming 2 cards is
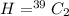
Generally the number of ways to select the 7 cards from the 52 deck of cards is
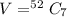
Generally the probability that exactly 5 of the 7 cards are hearts is mathematically represented as
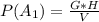
=>
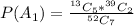
=>
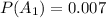
Considering question b
The number of ways to selected 3 diamonds out of the 13 diamonds is mathematically represented as
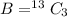
The number of ways to selected 3 hearts out of the 13 hearts is mathematically represented as

The number of cards that is not hearts or diamond is 52 - (13 +13) = 26
Generally the number of ways of selecting the reaming 1 cards is

Generally the probability that there are 3 hearts and 3 diamonds is
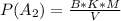
=>
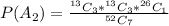
=>
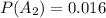
Considering question c
The number of ways to selected 1 spade out of the 13 spade is mathematically represented as
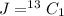
Generally the probability that there are 3 hearts, 3 diamonds and 1 spade is
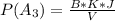
=>
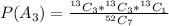
=>
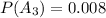
Considering question d
The number of ways to selected 2 Aces out of the 4 Aces is mathematically represented a
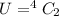
The number of ways to selected 2 Kings out of the 4 Kings is mathematically represented a
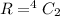
The number of cards that is not Aces or Kings is 52 - (4 +4) = 44
Generally the number of ways of selecting the reaming 3 cards is

Generally the probability that there are 2 Aces and 2 Kings is
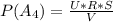
=>
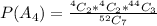
=>
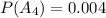
Considering question e
The number of ways to selected 3 Kings out of the 4 Kings is mathematically represented a
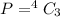
Generally the number of ways of selecting the reaming 2 cards is
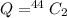
Generally the probability that there are 2 Aces and 3 Kings is

=>
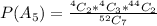
=>
