The value of theta is approximately 30.87 degrees.
To find the value of theta, we can use the properties of right-angled triangles.
In a right-angled triangle, one angle is always 90 degrees. The sum of the angles in any triangle is 180 degrees. Therefore, the sum of the other two angles in this triangle is 90 degrees.
We know one of the angles is theta. Let's call the other angle alpha.
Since the sum of theta and alpha is 90 degrees, we can write the equation: theta + alpha = 90.
To find the value of theta, we need to determine the value of alpha.
We are given that the sides of the triangle are 5 and 9.
The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Using this theorem, we can calculate the length of the hypotenuse:
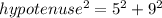



Now that we know the lengths of the sides, we can use trigonometric ratios to find the values of the angles.
The sine ratio is defined as the ratio of the length of the side opposite an angle to the length of the hypotenuse.
In this triangle, the side opposite theta is 5 and the hypotenuse is approximately 10.29.
So, sin(theta) = 5/10.29.
To find the value of theta, we can take the inverse sine (or arcsine) of this ratio:
theta = arcsin(5/10.29)
theta ≈ 30.87 degrees