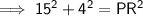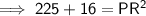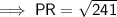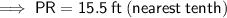Answer:
a) not safe
b) 15.5 ft (nearest tenth)
Explanation:
Part (a)
Tan trig ratio
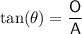
where:
 is the angle
is the angle- O is the side opposite the angle
- A is the side adjacent the angle
Given:
 = x
= x- O = PV = 4 ft
- A = RV = VQ = 15 ft
Substituting the given values into the formula and solving for x:
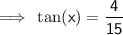
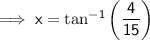
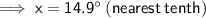
As 14.9° is not between 18° and 27°, the roof is not safe.
-------------------------------------------------------------------------------------------------
Part (b)
Pythagoras’ Theorem
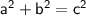
(where a and b are the legs, and c is the hypotenuse, of a right triangle)
Given:
- a = RV = VQ = 15 ft
- b = PV = 4 ft
- c = PR
Substituting the given values into the formula and solving for PR: