Answer:
The bottom-most spring going to be after three masses are hung on it is 14.3 cm
(a) is correct option
Step-by-step explanation:
Given that,
Three identical mass = 6.4 kg
Force constant = 7.8 kN/m
Distance before attached mass = 12 cm
We know that,
When we attached three identical masses then the total mass on the spring will be 3 mg.
We need to find the extension
Using balance equation
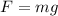

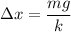
For three masses,
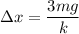
Put the value into the formula
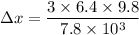
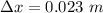
We need to calculate the length of the bottom spring
Using given length
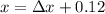
Put the value into the formula

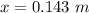
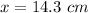
Hence, The bottom-most spring going to be after three masses are hung on it is 14.3 cm
(a) is correct option