Answer:
Make use of the fact that as long as
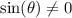 and
and
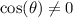 :
:
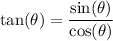 .
.
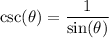 .
.
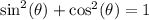 .
.
Explanation:
Assume that
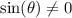 and
and
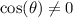 .
.
Make use of the fact that
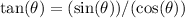 and
and
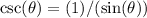 to rewrite the given expression as a combination of
to rewrite the given expression as a combination of
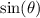 and
and
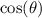 .
.
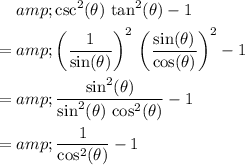 .
.
Since
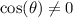 :
:
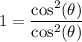 .
.
Substitute this equality into the expression:
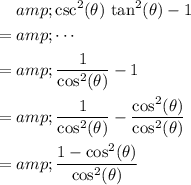 .
.
By the Pythagorean identity,
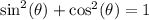 . Rearrange this identity to obtain:
. Rearrange this identity to obtain:
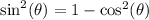 .
.
Substitute this equality into the expression:
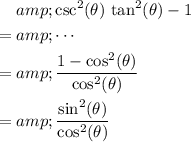 .
.
Again, make use of the fact that
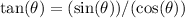 to obtain the desired result:
to obtain the desired result:
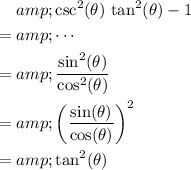 .
.