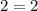Answer:

Explanation:
1) Use this rule:
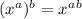 .
.
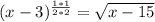
2) Simplify 1 * 1 to 1.
![\sqrt[2*2]{x-3} =√(x-15)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/9okt4t018pd6fv7svyvn.png)
3) Simplify 2 * 2 to 4.
![\sqrt[4]{x-3} =√(x-15)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/e4aw8aotmbv4js8bp7g5.png)
4) Square both sides.
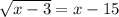
5) Square both sides.

6) Move all terms to one side.
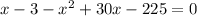
7) Simplify
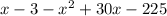 to
to
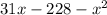 .
.

8) Multiply both sides by -1.
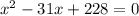
9) Factor
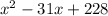 .
.
1) Ask: Which two numbers add up to -31 and multiply to 228?
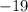 and
and
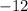
2) Rewrite the expression using the above.
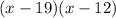
10) Solve for
 .
.
1) Ask when will
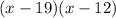 equal zero?
equal zero?
When
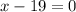 or
or
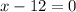
2) Solve each of the 2 equations above.

11) Check solution.
When
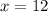 2, the original equation
2, the original equation
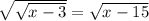 does not hold true. We will drop
does not hold true. We will drop
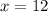 from the solution set.
from the solution set.
12) Therefore,

Check the Answer:
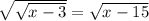
1) Let
 .
.
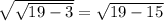
2) Simplify 19 - 3 to 16.
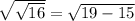
3) Since 4 * 4 is 16 6, the square root of 16 is 4.
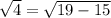
4) Since 2 * 2 = 4, the square root of 4 is 2.
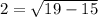
5) Simplify 19 - 15 to 4.
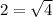
6) Since 2 * 2 = 4, the square root of 4 is 2.