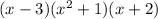Answer:
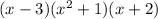
Explanation:
1) Factor
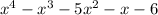 using Polynomial Division.
using Polynomial Division.
1 - Factor the following.
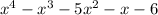
2 - First, find all factors of the constant term 6.
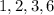
3 - Try each factor above using the Remainder Theorem.
Substitute 1 into x. Since the result is not 0, x-1 is not a factor..
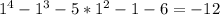
Substitute -1 into x. Since the result is not 0, x+1 is not a factor..
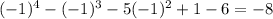
Substitute 2 into x. Since the result is not 0, x-2 is not a factor..
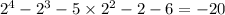
Substitute -2 into x. Since the result is 0, x+2 is a factor..
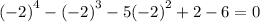
⇒
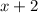
4 - Polynomial Division: Divide
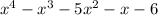 by
by
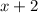
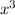
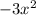

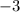
--------------------------------------------------------------
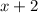 |
|
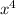
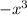
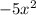
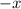
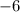
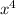
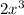
------------------------------------------------------------
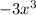
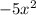
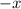
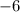
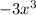
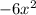
---------------------------------------
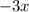
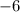
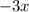
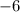
---------------
5 - Rewrite the expression using the above.
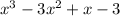
2) Factor out common terms in the first two terms, then in the last two terms.
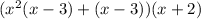
3) Factor out the common term
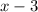 .
.